Table of Contents
Forward Error Correction (FEC)
FEC 的核心目標是傳送足夠量的冗餘資料以確保接收者能夠自己主動復原資料,而不需要發送者再次重傳資料!
※ 所有錯誤更正的目的就是達成「最小差距的解碼」,所有能達成此目的的解碼器都能更正至少 e 個錯誤 ( e < 1/2 (Dm-1),Dm 是兩字串間的最小差距,若 Dm 為偶數,則僅能做到錯誤偵測,若Dm 為奇數,則可做到錯誤更正)。
- Block codes
- Cyclic codes
- Reed-Solomon codes
- Convolutional codes
- Turbo codes
Hamming Distance (漢明距離)
定義:兩個字串中,對應位置但內容不同的字元總數。
範例:下列兩字串的漢明距離正好都是 2。
1011101 與 1001001
toned 與 rosed
在二進位中,正好就是將兩個二進位串一起做 XOR 運算之後,剩下多少個「1」,就表示漢明距離為多少。
Hamming Weight (漢明權重)
定義:一串符號中非零符號的總數。
在二進位中,整個二進位串中有幾個「1」就表示其漢明權重為多少。
Block Codes 分組碼
(n,k) 表示原始資料共有 k 個 bits,然後加上 n-k 個 bits 的檢查位元 (parity check bits) 後得到 n 個 bits 組成的區段碼,碼率 (Code rate R = k/n,即實際資料佔整組區段碼總長的比率),而當這種區段碼中的實際資料與校對碼為線性關係時,就稱之為線性區段碼。
線性區段碼的主要想法就是在資料之外,運用生成矩陣對原始資料做運算來額外添加一段作為校對用途的校驗碼,並使用校驗矩陣來修正傳輸過程中可能發生的錯誤。
(Linear) Block Codes 線性區段碼
參考資料一:http://web.ntpu.edu.tw/~yshan/intro_lin_code.pdf
參考資料二:http://jpkc.nwpu.edu.cn/dzjc/xiandaitongxin/jc/text/8.3.htm
線性碼 (Linear Codes) 的定義
假設 C = {0000.1111},則 C 為線性碼,因為可以從中挑出 X = 0000,Y = 1111,且 X+Y 所得到的 1111 也包含於 C 中。
如何判斷至少需要使用幾個 Parity Check Bits?
若 Parity Check Bits 的數量為 R,原始資料長度為 K,總資料長度為 N,則 2R ≧ K + R + 1。
Linear Block Codes 的基本運算方法
假設原有的資料為 abcd (每個字母代表一個 bit),使用 (7,4) Linear Block Code 後得到 abcdefg,由於 Parity Check Bits 會有 3 個,因此我們可以知道會有 3 條編碼方程式,且每次取四個原始資料中的三個來搭配一個校對碼:
A 組:a + b + c + e = 0 => A 式: a + b + c = e
B 組:a + b + d + f = 0 => B 式: a + b + d = f
C 組:a + c + d + g = 0 => C 式: a + c + d = g
由於上列式子,我們可以拆解出以下的組合: (若加起來進位則直接填入 0 )
| a | b | c | d | e | f | g | a | b | c | d | e | f | g |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
因此我們可以從中發現,透過 A、B、C 三組加總為 0 可以使用其中兩組就能判斷錯誤發生在哪個位元。
Linear Block Code 的矩陣運算方法 (一) 檢查矩陣 H
我們可以將上個部分的 A、B、C 三組以對齊方式寫成這樣:
1 x a + 1 x b + 1 x c + 0 x d + 1 x e + 0 x f + 0 x g = 0
1 x a + 1 x b + 0 x c + 1 x d + 0 x e + 1 x f + 0 x g = 0
1 x a + 0 x b + 1 x c + 1 x d + 0 x e + 0 x f + 1 x g = 0
就可以很容易地將係數表示成矩陣形式:
而由矩陣乘法的概念我們可以知道,上面這個矩陣乘上 [ a b c d e f g ]T 這個矩陣會得到一組全部都是 0 的矩陣,因此上面這個矩陣就是所謂的 檢查矩陣 (Parity Check Matrix,H),同時可以觀察到最右邊正好是一個 3×3 的單位矩陣,同時我們把左邊的矩陣稱為 P。
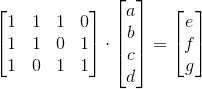
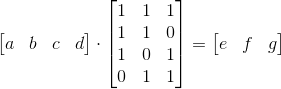
Linear Block Code 的矩陣運算方法 (二) 生成矩陣 G
我們可以將上上個部分的 A、B、C 三式,用類似的方法寫成矩陣:
接下來為了方便起見 (因為我們需要的是 [ a b c d ] 乘上一個矩陣後可得 [ a b c d e f g ] 的結果) 我們將等號左右兩側的矩陣同時轉置 (注意,乘法在轉置之後先後必須互換!)。
接下來我們在上面這個矩陣 (其實可以發現到它正好是上部分所提到的矩陣 P 的轉置 ) 左邊加上一個 4×4 的單位矩陣,正好就可以得到 [ a b c d e f g ] 的處理後字串了,我們稱這個矩陣為生成矩陣 (Generator Matrix,G)。
生成多項式 (Generator Polynomial)
生成多項式是另一種常用的生成矩陣表示方法,生成多項式具有下列明顯特徵:
- 最高項次方數為 N-K 次,也就是 R 次 (和校驗碼個數相等)
- 常數項為 1
- 所有其他碼多項式都會是生成多項式的倍式
因此我們可以使用二進位除法的方式找回生成矩陣的組成元素:
取下列式子的餘式就可以很簡單的得到生成矩陣中對應「列的數字組成」
(其中 R 為校驗碼個數,i 為由 0 起算到 k-1 的列別)
例如假設生成方程式 g(x) = 1 + x + x3,則可算出當 i = 0 時,餘式為 1 + x,表示成 [ 1 1 0 ]。
※ 請務必留意,這裡的除法是特殊的二進位除法,實際上運算類似於 XOR,即相同者填 0,相異者填 1,並沒有借位的概念。





![[下載] VMware ESXi 6.0 正式版 (GA)](https://isite.tw/wp-content/uploads/2015/03/vmware-partner-link-bg-w-logo-360x180.png)







![[CES 2019 速報] AMD 預覽下一代 “Zen 2” 處理器,可望成為本屆 CES 最大看點](https://isite.tw/wp-content/uploads/2019/01/AED8012-360x180.jpg)









![[教學] 使用 XperiFirm 製作 Xperia 手機原廠軟體 FTF 安裝包](https://isite.tw/wp-content/uploads/2016/04/XFX0001-360x180.png)















![[ 突發 ] Mega 創辦人呼籲大眾盡速備份 Mega 上的資料?! (附官方澄清)](https://isite.tw/wp-content/uploads/2016/04/AMU8563-360x180.jpg)


![[ WP 外掛 ] Duplicate Post 輕鬆一鍵將文章當成範本複製](https://isite.tw/wp-content/uploads/2016/04/wp-logo-360x180.png)









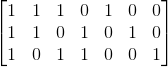
![[筆記] 憲法與政府體制 (三) 立法院行使各類職權所需立委席次數與黨團組成](https://isite.tw/wp-content/uploads/2016/10/SXS6051-350x250.jpg)
![[筆記] 計算機圖學概論:開發環境設定圖文教學](https://isite.tw/wp-content/uploads/2015/11/aurora-350x250.jpg)

![[筆記] 網路通訊原理:基本知識](https://isite.tw/wp-content/uploads/2015/03/6481980713_4d2950ae40_o-75x75.png)


